EL ENFOQUE DE LA UTILIDAD EN LAS DECISIONES
JUAN ANTONIO DEL VALLE F.
Hasta ahora hemos venido empleando el criterio del valor monetario esperado (VME) para seleccionar la mejor alternativa en los problemas de toma de decisión bajo condiciones de riesgo, criterio que no siempre convence a los tomadores de decisiones.
Todo mundo está consciente que el dinero tiene diferente significado entre las personas, entre las empresas, entre las instituciones y aún entre los países, además el significado del dinero para alguien en especial puede variar en el tiempo y no tener un valor constante.
Por consiguiente, lo que se propone en este Capítulo es usar una combinación de valor esperado y utilidad del dinero como medida de efectividad para seleccionar entre las alternativas.
4.1 Concepto de Equivalente Bajo Certeza.
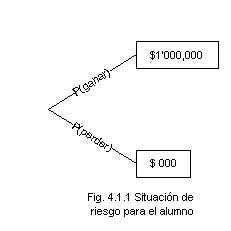
Al cuestionar por separado a dos alumnos de una clase de análisis de decisiones la siguiente situación. Suponga, se le pregunta a cada alumno, que usted es el dueño de un boleto de una rifa que tiene un 50% de posibilidades de obtener mil pesos; ¿Cuál es la cantidad mínima de dinero en que estaría dispuesto a traspasar el derecho a participar?. Se les anticipó a cada uno que era conveniente que no se apresuraran a dar una respuesta e hicieran la reflexión necesaria.
Después de un tiempo razonable, los alumnos respondieron de muy diversa manera. Uno de ellos estaba dispuesto a vender su boleto por $450,000 pero no por menos; el otro estaba dispuesto a venderlo por una cantidad mayor a $50,000.
¿ Está usted seguro ?, se le preguntó, que usted no podría aceptar vender su opción por menos de $ 450,000?; su compañero de clase podría estar dispuesto a vender el boleto por $50,000.
El alumno respondió que habría que "tenerle fé" al boleto y consideraba que su precavido compañero podría cambiar de opinión si el dinero estuviera sobre la mesa; esperaría que la respuesta del compañero cambiara si pensara un poco más en lo que podría obtener con ese millón de pesos.
El otro alumno defendió su posición de una manera semejante; este joven insistió en el límite de $50.00 e insinuó que su arriesgado compañero no tomaba la situación con la suficiente seriedad, ya que arriesgaba la venta del boleto al pedir $450.00 a cambio de sólo de una posibilidad.
Cada quien puede tener su propia opinión acerca de las respuestas de estos dos alumnos, sin embargo, es difícil hacer un estudio de sus conductas. Si tuvieramos que aconsejar a cada uno de ellos sobre que decisión tomar en un problema similar al propuesto, entonces mejor simplemente aceptemos el hecho de que ellos difieren en sus actitudes hacia el riesgo y que esas diferencias debieron influenciar sus respuestas.
Con los conceptos de los capítulos 1 y 2, se podría hacer un análisis comenzando por obtener un diagrama de árbol de decisiones, con los valores terminales y las probabilidades en los estados de la naturaleza. Suponga la siguiente lotería:

Una persona partidaria de VME calcularía lo siguiente:
0.5(1,000.00) + 0.5(0) = 500.00
para guiar su decisión. Sin embargo ahora estamos suponiendo que no siempre estamos de acuerdo con el VME y que, si nos ofrecieran intercambiar los derechos de esa opción por un poco menos de N$500,000 pudieramos aceptarlo. En esta forma, usted tiene una manera muy práctica de dar solución a este dilema; cada quien puede usar su propio juicio para decidir que cantidad específica quiere recibir en lugar de la rifa.
El alumno que fijó esa cantidad en N$450.00, estableció que si le fuera ofrecida una cantidad mayor a ella usted aceptaría en lugar de jugársela en la opción descrita; si le ofrecieran una cantidad menor a N$450.00 la rechazaría. En otras palabras, $450.00 es su equivalente bajo certeza, EBC, para esta lotería.
Usted aun puede decir que todo esto no está muy claro, porque $450.00 es realmente una cantidad muy cuestionable. Bien, imagínese que un vendedor ofrece el boleto de la lotería en venta y que alguien ofrece alguna cantidad X por la lotería citada. El vendedor requerirá instrucciones y no importará que tan subjetivo sea el costo, el alumno deberá decirle al vendedor: acepta una cantidad de N$450.00 o mayor, rechaza cualquier cantidad menor a ella.
Al analizar el problema de toma de decisiones, se cuenta ahora con un mejor consejero que es el EBC en lugar de seguir simplemente los dictados del VME, el cuál no es una guía completa para casi todas las personas en su toma de decisiones.
Por otra parte, existen diversas formas de transformar valores monetarios a valores de utilidad, siendo apropiado asociar con cada valor monetario su valor en esta nueva unidad y elegir la alternativa que tenga el mayor valor esperado sobre esta nueva escala de valores. Existen diferentes terminologías para las unidades de utilidad, siendo común llamarlas preferencias, útiles o utilidades a estas nuevas unidades.
La cuestión es determinar la forma que se harán las transformaciones monetarias a útiles.
4.2 El Concepto de Lotería.
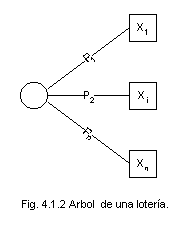
En la explicación del Equivalente Bajo Certeza se ha utilizado el concepto de lotería para significar una situación de riesgo, la cual tiene una probabilidad Pi de obtener un premio xi , donde i va desde 1 hasta n , siendo n el número de premios.
El conjunto de los premios es entonces X = {x1 ,.......,xn},
representándose una lotería L de la siguiente forma:
L = {(P1 ,x1 ), .........., (Pn ,xn )}
esto es, una lotería queda definida por el conjunto de pares ordenados (p1 ,x1 ), como se puede apreciar en la siguiente figura:
Los premios guardan entre sí una relación de preferencia o de utilidad, así cuando un premio i se prefiere a otro premio j, se simboliza como xi > xj , mientras que xi~ xj significa que el premio i es indiferente al premio j.
Las principales reglas lógicas para el manejo de premios y loterías son las siguientes:
- Sean xi y xj dos elementos del conjunto de premios X,entonces sólo se pueden tener una de las siguientes tres relaciones de preferencia: xi > xj ó xj > xi ó xi ~ xj.
- Si xi > xj y xj > xk , entonces es válido el principio de transitividad xi > xk .
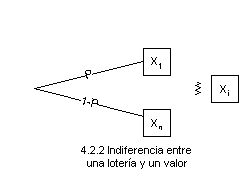
- Si se ordenan por su
preferencia los premios de X y si suponemos que xi
> ....... > xn , entonces para cada premio xi
de X diferente de x1 y xn , deberá haber
indiferencia entre tenerlo con certeza o bien jugar a la lotería
L' = {(p,x1),(1-p,xn )} si existe un valor
p; en forma gráfica esta regla se expresaría de la siguiente
forma:
Precio de venta de una lotería.
Es idéntico al equivalente bajo certeza de la lotería ,es decir,es la mínima cantidad que el decisor aceptaría por ceder (es decir,vender) sus derechos a participar en una lotería.
Ejemplo:
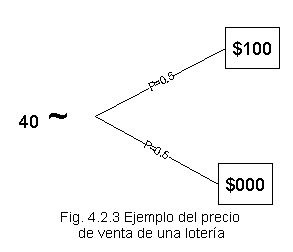
EBC = Precio de venta = $ 40
Precio de compra de una lotería.
Es la máxima cantidad que el decisor pagaría por participar en una lotería, la cual no necesariamente es la misma que el EBC.
Ejemplo: Si el precio de compra es $ 40 esto significa que
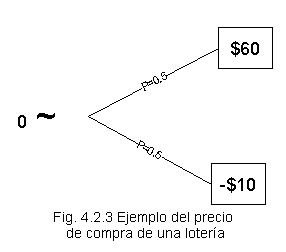
u(0) = 0.5u(60) + 0.5u(-10)
que claramente es distinto de la utilidad esperada en la lotería anterior (la del EBC) u(40) = 0.5u(100) + 0.5u(0)
4.3 Construcción de Curvas de Utilidad.
Para aplicar el enfoque utilitario a los problemas de decisión, es necesario contar con una función ó al menos con una gráfica que nos relacione las cantidades de dinero (o de unidades del atributo de interés) con la utilidad que asignamos a cada una de ellas.
El rango en unidades de utilidad en que puede variar el valor de la función puede ser totalmente arbitrario, sin embargo una práctica recomendable es considerar que las utilidades pueden variar entre cero y uno; a la cantidad mayor de dinero o al mejor valor terminal de algún atributo se le asigna el valor de uno, mientras que cero se le asigna a la menor cantidad de dinero o al peor valor del atributo.
Es conveniente advertir que para el diseño de la curva de utilidades es necesaria la opinión del decisor, ya que sólo él puede sintetizar todos los intereses que deben implicarse en una decisión, incluyendo las actitudes al riesgo.
En esta situación se puede decir que cada decisor deberá contar con su propia curva de utilidad, la cual es válida en un tiempo determinado para analizar los problemas de decisión de ese decisor precisamente.
Existen distintos métodos para la obtención de esas curvas, mismos que podemos clasificar por el tipo de cuestionamiento al decisor; algunos métodos cuestionan probabilidades mientras que otros se basan en preguntas sobre equivalentes bajo certeza para un conjunto de loterías.
Método Cuestionando Probabilidades.
Sea X = {xo , x1 , ..... , xn , x* } el conjunto de resultados terminales de cualquier problema de decisiones y supongamos las siguientes relaciones de preferencia entre estos valores: x*>xi>x0, donde i=1,....,n.
Además supongamos que se le asignan utilidades arbitrarias a xo y x* de cero y uno respectivamente:
u(xo) = 0 y u(x*) = 1
Ahora para cualquier xi se cumple lo siguiente: 1=<u(xi)=<0.
El método consiste en cuestionar al decisor sobre probabilidades que para él hagan indiferente recibir una cantidad xi ó jugar a la siguiente lotería: L = {(p,x*),(1-p,x0)}.
Vista la situación de otra forma se le pide al decisor declare un valor p tal que las dos alternativas del siguiente árbol de decisiones le sean indiferentes:
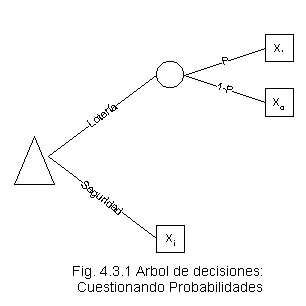
esto es :
u(xi ) = p u(x* ) + (1-p) u(x0 )
Estas preguntas se repetirían para diferentes valores de xi , hasta obtener un número de valores de la función que permitan dibujar la curva con la exactitud deseada. Usualmente son 5 los puntos a obtener para dibujar la curva.
Ejemplo 3.3.1
Se tiene el siguiente problema de decisiones:
Se propone dos contratos a la empresa constructora A.B.C ; el primero le puede generar una de estas utilidades, con sus respectivas probabilidades:
Gananciasen millonesde pesos |
Probabilidades |
| 80.00 | 0.6 |
| 50.00 | 0.2 |
| 10.00 | 0.15 |
| - 6.00 | 0.05 |
El contrato número dos le puede generar utilidades por:
| Ganancias en
millones de nuevos pesos |
probabilidades |
| 100.00 | 0.40 |
| 25.00 | 0.50 |
| - 30.00 | 0.10 |
Otra alternativa es el no aceptar ningún contrato.
Resolver el problema tomando en cuenta las preferencias del gerente de A.B.C.
Solución.:
El problema puede plantearse así:
A1 : Seleccionar el contrato 1.
A2 : Seleccionar el contrato 2.
A3 : No aceptar ninguno.
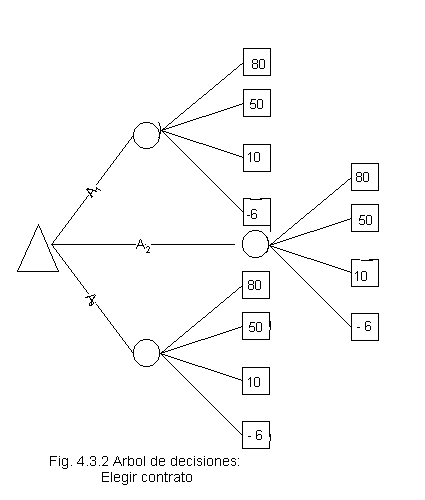
El conjunto de resultados posibles en orden de preferencia es:
X={ 100,80,50,25,10,0,-6,-30 }
El mejor resultado es X* = 100. El peor resultado es Xo = -30.
Aplicando el método cuestionando probabilidades:
u(100) = 1.0 u(-30) = 0.0
Para Xi =80 se debe encontrar un valor de P tal que haya las dos ramas del siguiente árbol equivalentes:
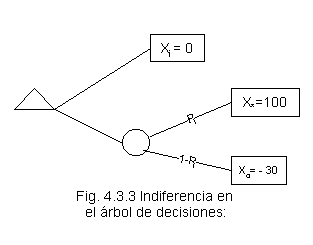
Entrevistando al Gerente General. de A.B.C.:
Nos dice que P = 0.95, entonces u(80) = 0.95(1) + 0.05(0)
por lo tanto :
u(80) = 0.95
El procedimiento se repite para Xi = 50, 25, 10, 0, -6 y se obtienen las siguientes cantidades:
u(50) = 0.80 u(25) = 0.65
Este conjunto de valores es la función utilidad del Gerente General.de A.B.C.
u(10) = 0.55 u(0) = 0.40 u(-6) = 0.35
Graficando Tenemos:
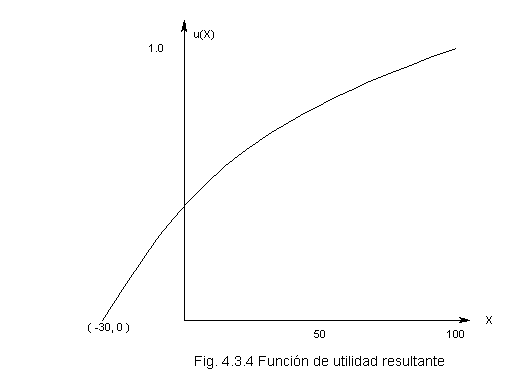
Método Cuestionando Equivalentes Bajo Certeza.
Un método diferente para evaluar las curvas de utilidad es utilizando declaraciones de equivalentes bajo certeza a un conjunto de loterías. Entre estos métodos se encuentra el del Tetraedro ,el cual consiste en pronosticar la cara que queda contra el piso.
Los supuestos iniciales son los mismos que los explicados antes, solo que ahora se pediría al decisor declarar los equivalentes bajo certeza para las siguientes loterías:
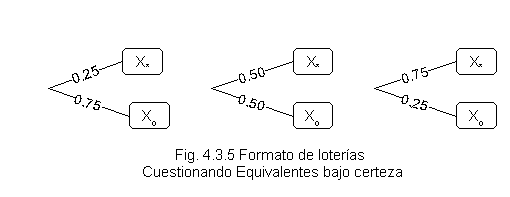
Evaluando las utilidades para los equivalentes bajo certeza se tienen los siguientes resultados :
u(EBC ) = 0.25x* + 0.75xo = 0.25
u(EBC ) = 0.50x* + 0.50xo = 0.50
u(EBC ) = 0.75x* + 0.25xo = 0.75
Con estos tres puntos y los dos supuestos ( X*=1 y xo =0) se tienen cinco puntos, cantidad mínima acostumbrada para trazar la curva.
3.4 Análisis de las Actitudes del Decisor.
El análisis de la curva de utilidad de un decisor permite identificar su actitud hacia el riesgo, siendo posible detectar la aversión, la indiferencia y la propensión.
Prima de Riesgo.
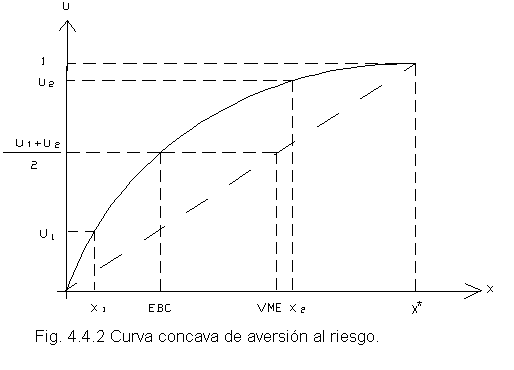
Este concepto es de utilidad para calificar la actitud hacia el riesgo y se define como la diferencia entre el valor monetario esperado y el equivalente bajo certeza.
PR = VME - EBC
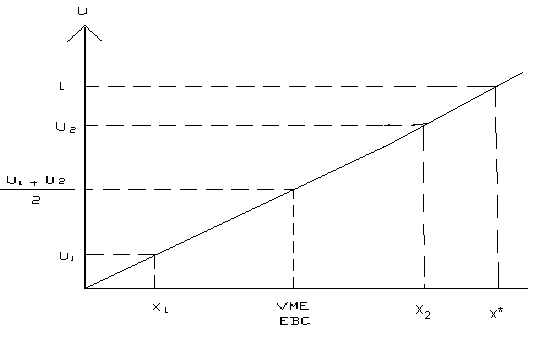
El signo positivo de la prima de riesgo significará que el EBC se sitúa en la gráfica de la curva a la izquierda del VME y la forma de la curva es de tipo cóncava respecto al eje de las abcisas, véase la siguiente figura; la prima de riesgo en este caso representa la cantidad que el decisor está dejando de ganar por su aversión al riesgo. Sea la siguiente lotería:
Si graficamos en una curva cóncava de aversión al riesgo, los puntos x1 y x2, y se les asignan respectivamente las utilidades u1 y u2 , se puede observar que la prima de riesgo resulta positiva.
Si la prima de riesgo es igual a cero, significa que el decisor se rige por el criterio del valor monetario esperado y no toma en cuenta al riesgo; la curva de utilidades en este caso es una recta, existiendo una relación lineal entre el atributo y su utilidad:
Cuando la prima de riesgo es negativa significa que el decisor está dispuesto a pagar esa cantidad por participar en la situación de riesgo; en este caso la curva resulta de tipo convexa y se puede observar que al graficar los puntos de la lotería y sus utilidades correspondientes en esa curva, el equivalente bajo certeza se sitúa a la derecha del valor monetario esperado, como puede verse en seguida:
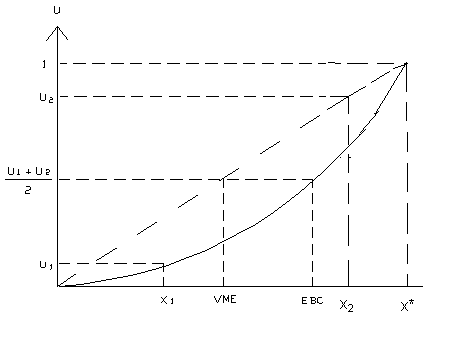
Es conveniente hacer notar que las consideraciones anteriores son válidas para el caso de funciones crecientes, la situación se invierte cuando la función es de tipo decreciente; en el caso de funciones decrecientes las curvas cóncavas denotan propensión mientras que las convexas indicarán aversión.
La determinación precisa de una función de utilidad requiere que primero se conozca cual es su forma general, para lo que debe verificarse que las preferencias del decisor satisfagan ciertos criterios, los cuales restringen la forma de la función de utilidad. Para ello es útil obtener una expresión cualitativa de sus preferencias, para después escoger la función de utilidad específica que satisfaga los requerimientos de forma y que además sea consistente con unos cuantos valores de µ(x) que hallan sido evaluados de manera cuidadosa.
4.5 Problemas propuestos
Problema 1.
Un ingeniero constructor para ejecutar unos trabajos de terracerías analiza las alternativas de rentar, comprar o utilizar su mismo equipo para cumplir con un cierto contrato que ya obtuvo.
El ingeniero mantiene la espectativa de que exista una ampliación del contrato al doble o al menos de un 50%, eventos que se estiman sucedan con probabilidades de 0.35 y 0.40, siendo la probabilidad de que no se extiendan los trabajos de 0.25.
Con el contrato actual, el ingeniero estima una utilidad de 500, -1300 y 1000 millones de pesos en forma correspondiente con cdad una de las alternativas mencionadas, rentar, comprar o reutilizar.
Si se ampliaran los trabajos al doble, las expectativas de utilidad serían 1000, 2000 y -1500 millones de pesos y si solo se contratara un 50% mas entoces estos valores serían 750, 1000 y -900 millones de pesos.
1) Para personalizar el ejercicio, considerese el ingeniero del problema y construya su curva de utilidades por cualquiera de los métodos vistos en clase. Explique demás cual es el comportamiento hacia el riesgo que denota la curva, por sectores si es necesario.
2) Obtenga el árbol de decisiones que explique el problema de toma de decisión.
3) Usando un criterio monetario recomiende una decisión y explique cuales serían las limitaciones de este criterio.
4) Usando un criterio utilitario recomiende la decisión.
Problema 2.
Considerese usted en el lugar del Director de PEMEX y que desea construir la curva de utilidad de la empresa, para la cual se le cuestiona sobre los precios mínimos de venta que daría a las siguientes loterías:
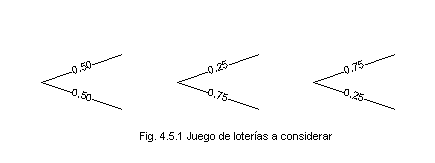
a) Obtenga la curva de utilidades, considere una forma lineal entre los puntos.
b) Describa sus actitudes hacia el riesgo, justificando su respuesta.
c) Que zonas del plano coordenado de la curva deben cancelarse y por que razones.
Problema 3.
PEMEX debe decidir la perforación de un pozo en un sitio determinado. El costo de la perforación es de 100 millones de dólares, independientemente de si existe o no petróleo. Si hay petróleo se estiman ganancias por ventas de 600 millones de dólares.
PEMEX tienen el recurso de mandar hacer un estudio geológico del sitio, mismo que le cuesta 10 millones de dólares y le revelará con absoluta certeza si el terreno es de tipo A, B ó C, los cuales tienen distintas posibilidades de contener petróleo:
P(A/petróleo) = 14/28
P(B/petróleo) = 5/28
P(C/petróleo) = 9/28
Las probabilidades apriori de que el terreno sea de un tipo determinado son:
P(A) = 0.2 P(B) = 0.3 P(C) = 0.5
La probabilidad de apriori de encontrar petróleo es 0.28
a) Diseñe el árbol de decisiones.
b) Calcule las probabilidades necesarias.
c) Utilizando los criterios monetario y utilitario (usando la curva del problema 2). Recomiende la mejor decisión.